- カテゴリ
まずは、前回の数学(微分法(数学Ⅱ))の解説から!
前回の問題 数学(微分法(数学Ⅱ))
<問題>
|
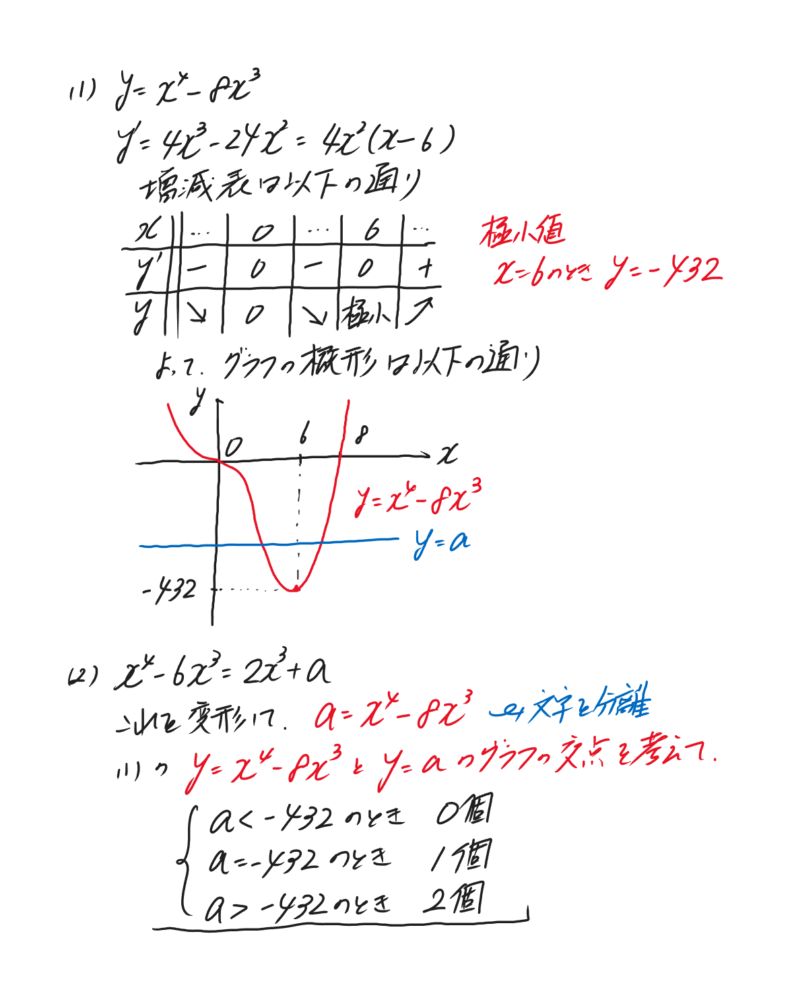
曲線y=x4-8x3について、以下の問いに答えよ。 (1)曲線y=x4-8x3の増減を調べ、概形を描け。 (2)x4-6x3=2x3+aの異なる実数解の個数を求めよ。 |
<ヒント>
(1)微分して増減表を書き、極値を求めましょう。
(2)は(1)のグラフを利用しましょう。
<解答>
今回は、簡単だったと思います。文字を分離(文字=□ の式に変形すること)して、グラフの交点を考えることは、色々な場面で使います。
今週の問題 物理(波動)
<問題>
|
平面ガラスの上に曲率半径Rの球面をもつ平凸レンズを載せて、上から波長λの単色光を当てる。その結果、平面ガラスと平凸レンズの接触点をOとすると、点Oを中心とする同心円状のニュートンリングが観察される。 (1)接触点Oから平面ガラスに沿って距離rだけ離れた点における、平面と球面の間隔hをrとRを用いて表せ。但し、hはrに比べて十分小さいものとする。 (2)平凸レンズの上からニュートンリングを見た場合、干渉縞の明るさが極大となる円の半径を自然数nを使って答よ。 (3)平面ガラスの下からニュートンリングを見た場合、干渉縞の明るさが極大となる円の半径を自然数nを使って答よ。 |
<ヒント>
(1)図を描いて、三平方の定理を使いましょう。
(2)(3)反射による位相のズレと光の道筋の光路差(光路差=媒質の屈折率×経路差)と波長の関係を考えましょう。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら