---

　まずは、前回の数学（微分法・積分法）の解説から！

前回の問題　数学（微分法・積分法）

＜問題＞

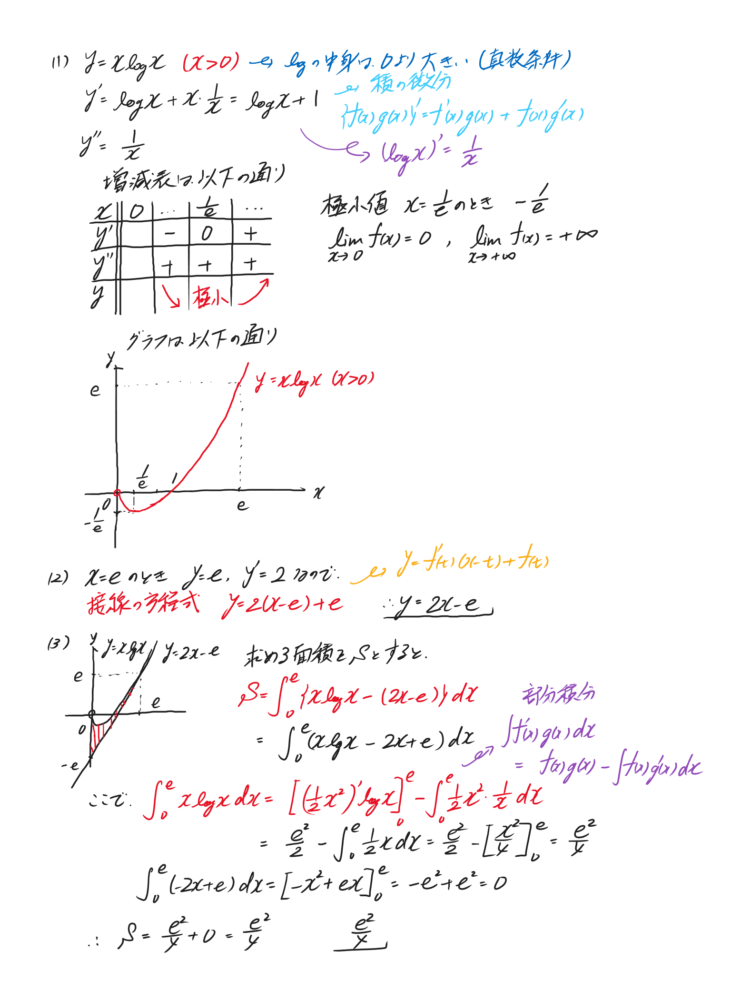
関数y=xlogx (x>0)において （1）グラフの増減、凹凸、極値、変曲点を調べ、グラフの概形を描け。ただし、この関数のx→+0の極限は0であることを用いても良い。 （2）y=logx上の点(e,e)における接線の方程式を求めよ。 （3）関数y=xlogx (x>0)と（2）の接線、y軸とで囲まれた部分の面積を求めよ。

＜ヒント＞

（1）増減表を描きましょう。（3）部分積分を利用しましょう。

＜解答＞

　部分積分のときは、符号に注意しながら行って下さいね。

今週の問題　数学（微分法・積分法）

＜問題＞

関数y=e-xsinx (0≤x≤2π)とx軸とで囲まれた部分の面積を求めよ。

＜ヒント＞

まずは不定積分を2回部分積分をすることで求めましょう。

　学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。