- カテゴリ
まずは、先週の数学(微分法(数学Ⅱ))の問題の解答から。
最大・最小の問題は場合分けが必要なものが多いので気を付けて下さいね。
先々週の問題 数学㉔(微分法(数学Ⅱ))
<問題>
| 関数f(x)=x3-ax2 (-2≤x≤2)の最大値と最小値を求めよ。但し、aは正の定数とする。 |
<ヒント>
取り敢えず、微分なんだけども、定義域に極値が含まれるかどうかの場合分けはして下さいね。あと、極値と定義域の両端での値の大小関係を比較して考えましょう。
<解答>


今週の問題 物理⑫(運動方程式)
<問題>
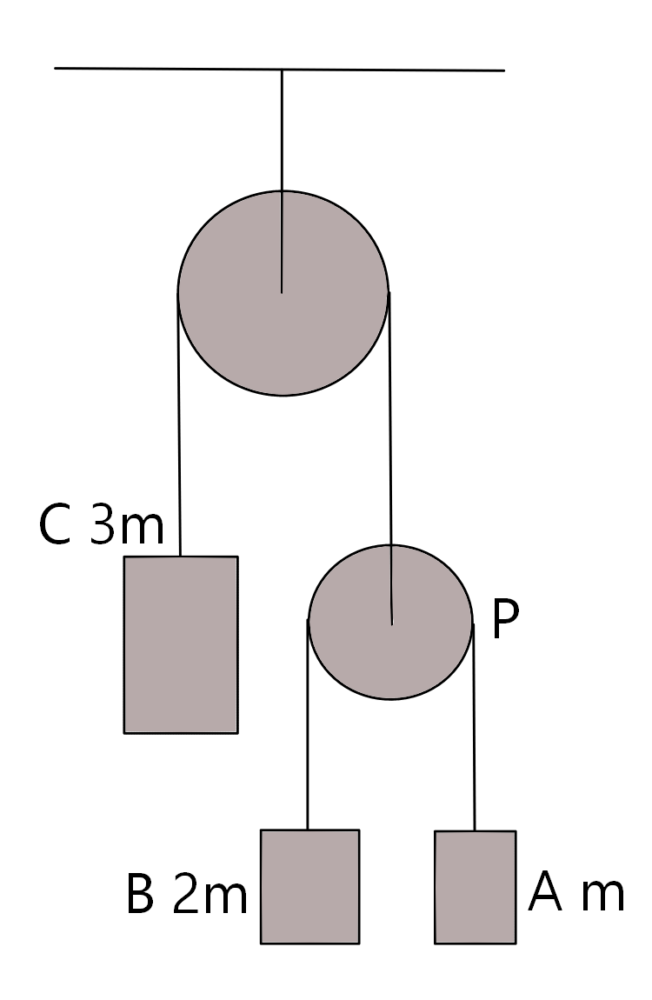 質量m,2m,3mのおもりA,B,Cを図の様に、滑車にかけて放す。Cの加速度を下向きを正、A,Bの加速度を上向きを正とし、A,B,Cそれぞれの加速度をa,b,cとする。AとBをつなぐ糸の張力をT、Cと同滑車Pをつなぐ糸の張力をSとする。A,B,C,Pの運動方程式とa,b,cに成り立つ関係(束縛条件)を書き、cとTを求めよ。但し、重力加速度をg、滑車と糸の質量は無視するものとする。 質量m,2m,3mのおもりA,B,Cを図の様に、滑車にかけて放す。Cの加速度を下向きを正、A,Bの加速度を上向きを正とし、A,B,Cそれぞれの加速度をa,b,cとする。AとBをつなぐ糸の張力をT、Cと同滑車Pをつなぐ糸の張力をSとする。A,B,C,Pの運動方程式とa,b,cに成り立つ関係(束縛条件)を書き、cとTを求めよ。但し、重力加速度をg、滑車と糸の質量は無視するものとする。 |
<ヒント>
Cの質量がAとBの質量の合計と等しいからと言って、つり合うわけではないですよ。きちんと物体毎に運動方程式を立てて下さい。又、束縛条件は、AとBが糸でつながり、CとPも糸でつながっているので、Cの変位=Pの変位、Pから見たAの上昇分=Pから見たBの下降分(AのPに対する相対変位=PのBに対する相対変位)の関係から考えて下さい。この辺りは、絵を描くとわかると思います。あとは、カリカリと計算して下さいね。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら

