- カテゴリ
まずは、前回の数学(領域)の解説からです。
先週の問題 数学㊶(領域)
<問題>
|
x+3y≥3…① x-y≥-1…② 5x-y≤15…③ 上記3つの不等式を満たす領域を満たしながら、点P(x,y)が動くとき、x2-2x+y2+4yの最大値と最小値を求めよ。 |
<ヒント>
まずは、領域を図示しましょう。x2-2x+y2+4y=kとおきます。これは円の方程式になりますので、中心から図示した領域まで、最長と最短となる点を考えれば良いわけです。
<解答>
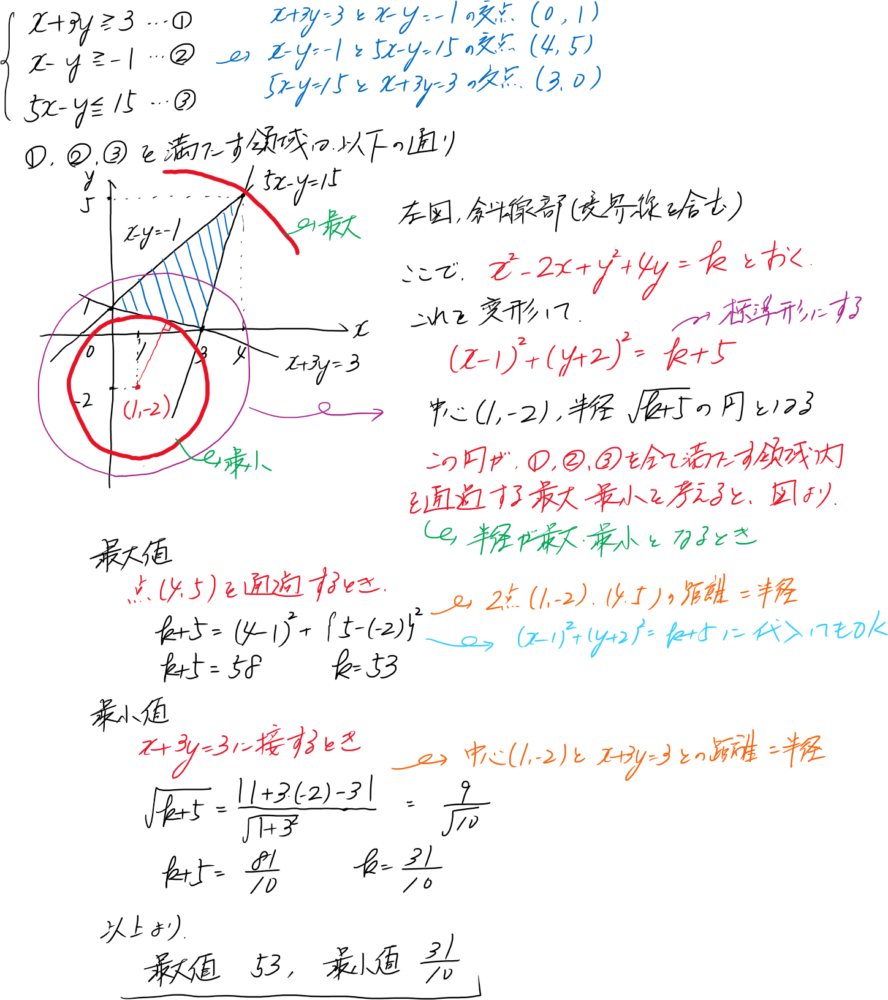
今週の問題 数学㊷(三角関数)
<問題>
|
0<θ<πとする。4sinθcosθcos3θ=sin3θを満たすとき、sinθ、sin2θ、sin4θの値を求めよ。 |
<ヒント>
3倍角の公式を利用して、cos3θ、sin3θを直しましょう。そして、頑張ってsinθだけの式にして、sinθの高次方程式を解きましょう。その後は、2倍角の公式を利用して、sin2θとsin2θの値を求めます。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら

