- カテゴリ
まずは、前回の数学(微分法)の解説から!
前回の問題 数学(微分法・積分法)
<問題>
|
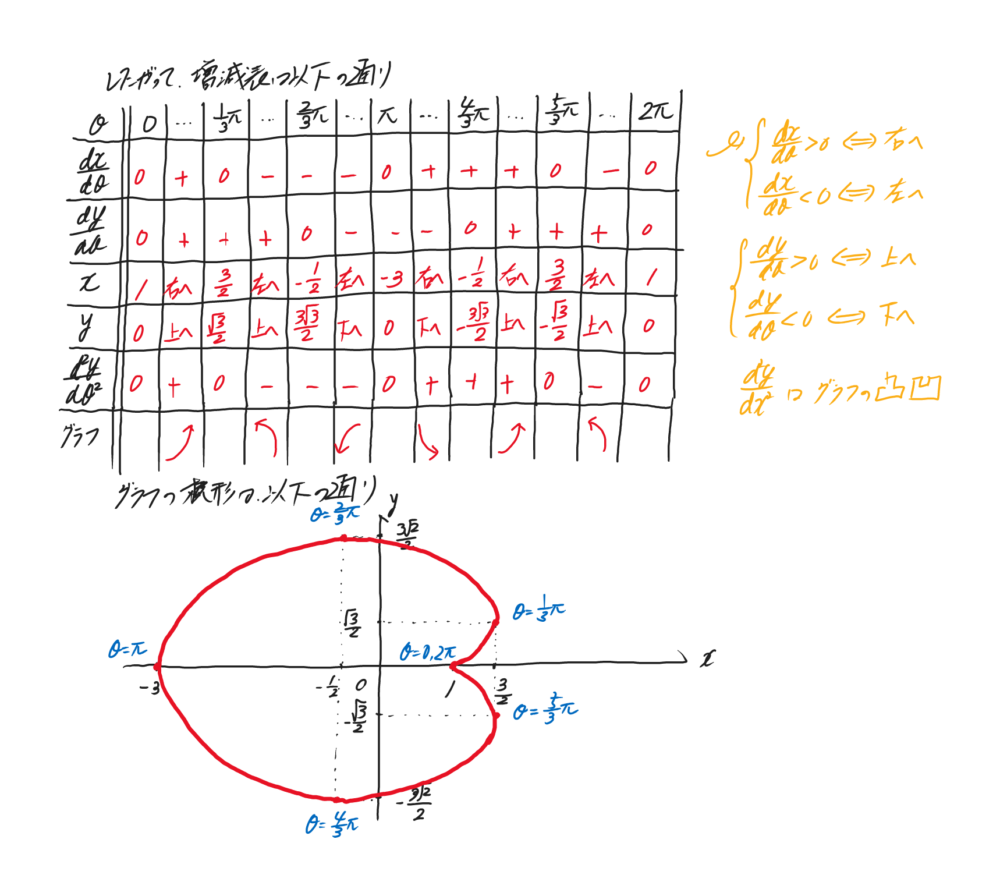
媒介変数関数 x=2cosθ-cos2θ, y=2sinθ-sin2θ (0≤θ≤2π)の概形を描き、その曲線の長さを求めよ。 |
<ヒント>
概形は、dx/dθとdy/dθを求めその符号の変化を調べましょう。
dx/dθが正なら右へ、負なら左で移動します。同様に、dy/dθが正なら上へ、負なら下へ移動します。
そして、頑張って凹凸も調べましょうね。d2y/dx2=d2y/dθ2×1/(dx/dθ)を計算しましょう。
曲線の長さは、公式通りです。只、グラフの対称性を利用すると計算が楽になるでしょう。
<解答>
すごく手間が掛かったと思います。計算量が多くて大変でしたね。微分した後の符号を調べるのに骨が折れると思いますが、頑張って計算しましょう。
今週の問題 物理(原子核)
<問題>
|
α粒子を軽い元素に衝突させると、電気的に中性で透過力の高い粒子が発生する。この粒子は電荷を持たないが、他の原子核と衝突すると運動エネルギーを与えるため、衝突された原子核の飛跡を観測できる。この中性粒子を異なった2種類の原子核に同一速度で衝突させた。衝突は弾性衝突とし、中性粒子の質量をm、速度をv、原子核の質量をM、最初、原子核は静止していて、衝突は1次元で起こるものとする。 (1)衝突された原子核の速度Vを求めよ。 (2)水素、及び窒素の原子核と中性粒子の衝突後の飛跡を観測したところ、それぞれの速度を観測したところVH=3.3×107m/s、VN=4.4×106m/sだった。速度の比VH/VNをmと水素原子核の質量MHと窒素原子核の質量MNを用いて答よ。 (3)水素原子核と窒素原子核の質量数はそれぞれ1と14である。中性粒子の質量数を求め、この中性粒子の正体を求めよ。 |
<ヒント>
(1)運動量保存則とエネルギー保存則から求めましょう。
(2)(1)の結果を利用。
(3)(2)の結果を利用。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。