まずは、化学の解答・解説からです。今回から、＜ヒント＞も残して問題を書きますね。

 

＜問題＞

容積が自由に可変できる容器に0.600molの窒素と0.400molのエタノールを封入した。42℃、62℃におけるエタノールの飽和蒸気圧は、それぞれ0.200atm、0.500atmである。気体定数を0.082atm・l/mol・Kとする。設問には、有効数字3桁で答えよ。 [実験1]　容器内の温度を62℃、全圧を1.000atmに保つ。 [実験2]　温度を62℃に保ったまま、全圧を増加させる。 [実験3]　容器内の温度を42℃、全圧を1.000atmに保つ。 （1）実験1の結果、容器内の体積は何lになるか。 （2）実験2において、液体のエタノールが生成し始めるときの容器内の体積は何lか。 （3）実験3の結果、容器内の体積は何lか。又、エタノールが何％液化するか。但し、液体の体積は無視する。

 

＜ヒント＞

「液体が存在するのか？」それとも、「すべて気体なのか？」を蒸気圧の問題では確認する必要がある。

計算上でのエタノールの分圧≧その温度での飽和蒸気圧⇔エタノールは一部液体

計算上でのエタノールの分圧＜その温度での飽和蒸気圧⇔エタノールはすべて気体

（1）は上記のことを考える。

（2）は、エタノール一部が液体となり始めるのは、分圧が飽和蒸気圧と等しいとき。これを利用する。

（3）は、う～ん。これは、自力で考えてみて。

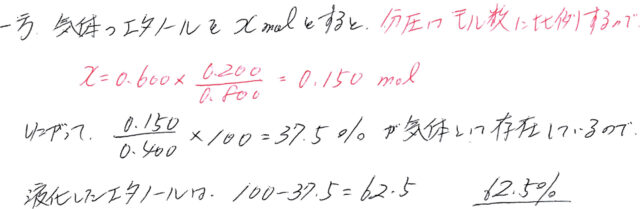
理想気体の状態方程式は、呪文の如く覚えることです。あとで、物理の公式解説で説明予定ですけどね。

では、続いて、数学の問題。今回は、曲線の長さです。

＜問題＞

原点を中心とする単位円がある。長さ2πの糸の一端を円周上の点A(1,0)に固定し、他端をPとする。Pは最初、点P0(1,2π)に位置し、この状態から、糸がたるまないように引っ張りながら点Pを反時計回りに回転して、単位円に巻き付ける。このとき、点PはP0から点Aまで動くことになる。糸は伸び縮みしないものとして、このときの点Pの描く軌道の長さを求めよ。

＜ヒント＞

　取り敢えず、図を描いてみてね。

　糸と単位円の接点をT(cosΘ，sinΘ)とでもおくと、弧ATの長さがΘになるよね。だからPTの長さは2π-Θだ。直線PTが接線となるから、半径OTは直交するよね。これを利用して、ベクトルTPを表すわけです。そうすれば、ベクトルOP、すなわち点Pの位置ベクトルをΘを使って表せる。（媒介変数表示ができたわけだ！）あとは、曲線の長さの公式を使おう。

　曲線の長さの公式は、きちんと理解＆暗記をしておくように。

　受験や学習に関する質問はお気軽にどうぞ！問い合わせフォームからお願いします。