- カテゴリ
まずは、先週の物理(単振動)の解説からです。
今週の問題 数学(軌跡)
<問題>
|
|
<ヒント>
2つの小球の位置をそれぞれx1、x2として運動方程式を立て、初期条件から求めて行こう。難しくはありますが、単振動の基本に沿って行えば、解けますよ。
<解答>

図を描いて、おもりの位置からばねののび(縮み)を考えて、運動方程式を立てることができる。そして、初期条件を変位、速度の式に代入して係数を求める。この2つができれば、あとは簡単です。とは言っても、運動方程式を立てるのは、この問題は難しいですよね。では、化学です。熱化学方程式をやりましょう。
今週の問題 化学(熱化学方程式)
<問題>
以下の結合エネルギー、生成熱、昇華熱の値を利用して答よ。
| 結合 | N≡N | H―H | N-H | C-H |
| 結合エネルギー〔kJ/mol〕 | 946 | 436 | 391 | 412 |
| 物質 | プロパン C3H8(気) | 黒鉛 C | プロペン C3H6(気) |
| 反応熱の種類と値〔kJ/mol〕 | 生成熱 105 | 昇華熱 717 | 生成熱 ー20 |
(1)アンモニア(気体)の生成熱を求めよ。
(2)C―C結合エネルギーを求めよ。
(3)C=C結合エネルギーを求めよ。
<ヒント>
(1)アンモニアの生成反応を書いて、求める生成熱をQ1とする。
表から、N2=2N-946kJ /molなどの式ができるので、それからQ1を求めよう。
もしくは、エネルギーの図(縦軸をエネルギー)を描いて、求めよう。
(2)エネルギーの図を描くと、分かると思います。
(3)(2)の結果を利用してください。
分子内の結合の数には注意して下さいね。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。

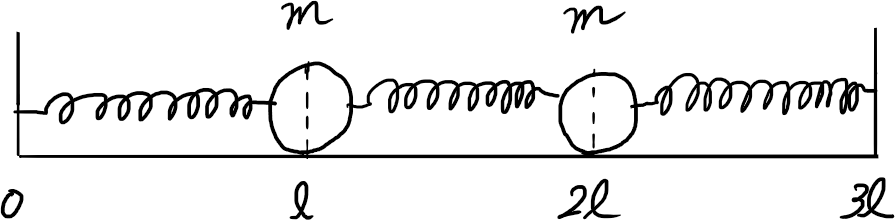 図のように、3個のばね定数kの等しいばねと2個の小球(質量m)を一直線につなぎ、水平で滑らかな台の上に置き、両端を固定した。静止の状態では、ばねは全て自然長であり、小球は図のような位置にある。静止の状態から、x=lにある小球をそこから右にaだけ、x=2lにある小球をそこから左にaだけずらして、同時に離したときの振動の周期を求めよ。
図のように、3個のばね定数kの等しいばねと2個の小球(質量m)を一直線につなぎ、水平で滑らかな台の上に置き、両端を固定した。静止の状態では、ばねは全て自然長であり、小球は図のような位置にある。静止の状態から、x=lにある小球をそこから右にaだけ、x=2lにある小球をそこから左にaだけずらして、同時に離したときの振動の周期を求めよ。