まずは、前回の化学（結晶構造）の解説から！

前回の問題　化学（結晶構造）

＜問題＞

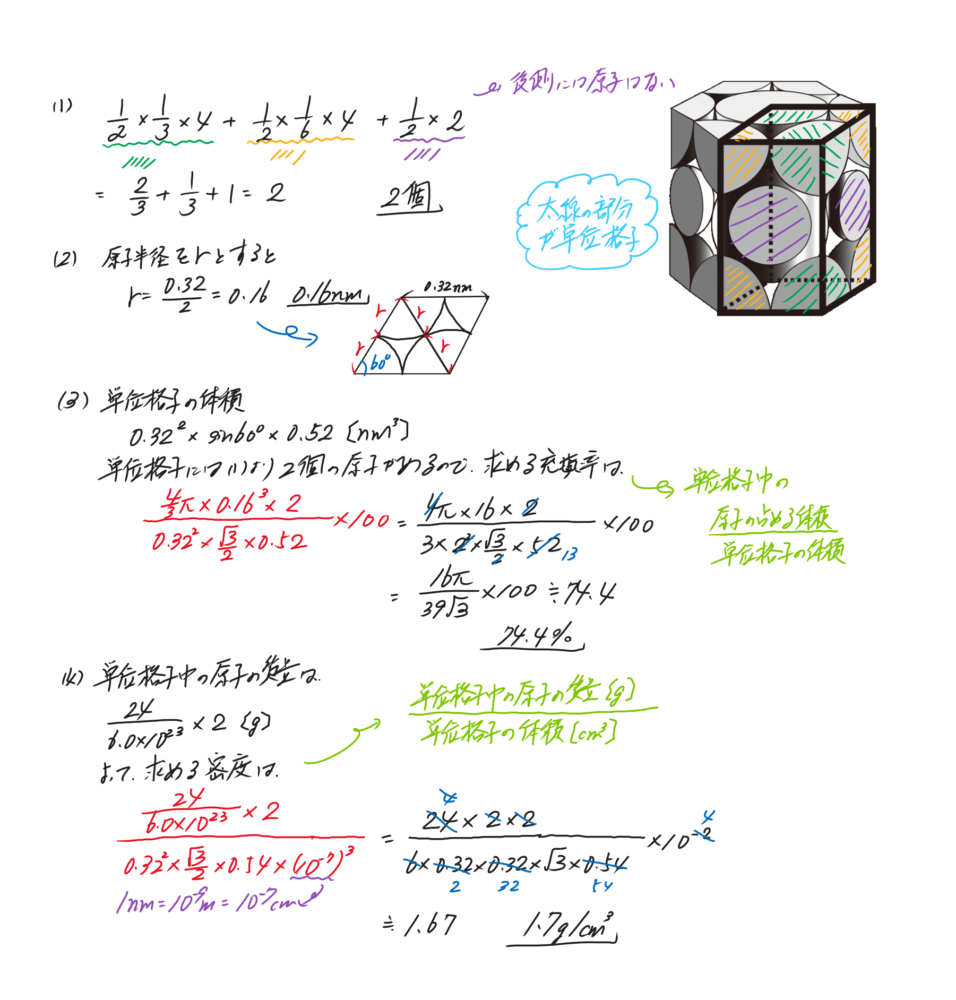
マグネシウムの単体は六方最密構造をとり、底面の正六角形の一辺の長さは0.32nm、高さは0.52nmである。マグネシウムの原子量を24、アボガドロ数を6.0×1023/molとして以下の問いに答えよ。 （1）単位格子中のマグネシウムの原子数を求めよ。但し、この場合の単位格子は底面が一辺0.32nmのひし形、高さが0.52nmの四角柱とする。 （2）マグネシウム原子の半径を求めよ。 （3）六方最密構造の充填率を求めよ。 （4）マグネシウムの結晶の密度[g/cm3]を求めよ。

＜ヒント＞

（1）六方最密構造の図を描きましょう。そして、原子数を計算しましょう。

（2）底面の正六角形を描いてみましょう。

（3）単位格子中の原子の体積/単位格子の体積を計算します。

（4）（1）の結果から単位格子の質量を求めれば密度は求められます。

＜解答＞

　六方最密構造は他の単位格子と比べると出題頻度は低いですが、面心立方構造と同じく最密構造であることは知っておいて下さいね。

今週の問題　数学（多項定理）

＜問題＞

(a+b+1/a+1/b)8 を展開したときのa3bとa5bの係数を求めよ。

＜ヒント＞

展開したときのa,b,1/a,1/bの次数をそれぞれp,q,r,sとすると、それぞれの項は、

8!/p!q!r!s!×a^pb^q(1/a)^r(1/b)^s （p+q+r+s=8)ですね。

　学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。