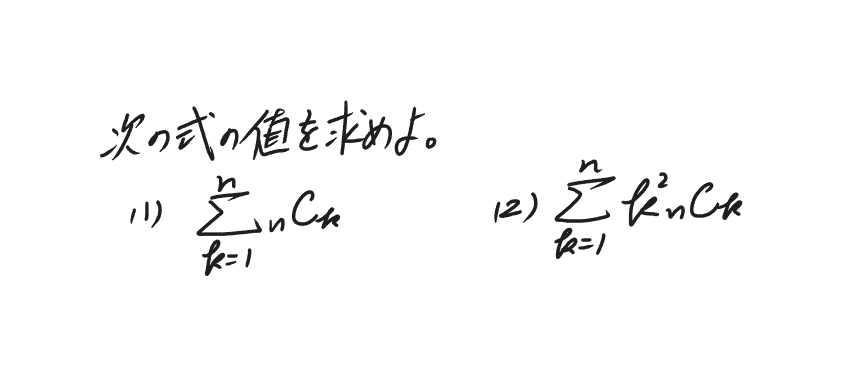- カテゴリ
まずは、前回の数学(多項定理)の解説から!
前回の問題 数学(多項定理)
<問題>
|
(a+b+1/a+1/b)8 を展開したときのa3bとa5bの係数を求めよ。 |
<ヒント>
展開したときのa,b,1/a,1/bの次数をそれぞれp,q,r,sとすると、それぞれの項は、
8!/p!q!r!s!×apbq(1/a)r(1/b)s (p+q+r+s=8)ですね。
<解答>
多項定理とか二項定理は順列を思い出してもらえれば良いですよ。他項定理は重複を許して複数のものを並べる方法ですし、二項定理は2つのものを重複を許して並べる方法と考えてしまえば良いです。只、そこに微分とかが絡むとなかなか厄介です。
今週の問題 数学(二項定理)
<問題>
|
|
<ヒント>
(1)(1+x)nを展開して二項定理を考えましょう。
(2)(1+x)nを展開した式をxで微分して、更にxをかけてもう一度微分してみてください。そうすればk2の部分が出てきますよ。正直(2)は難しいです。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら