- カテゴリ
まずは、数学の解答・解説。
区分求積法の問題は、
①∑の前に1/nを出す。
②∑の中をk/nの関数にして、k/n=xおく。
③0~1の範囲で(k=1は0に、k=nは1に対応)で積分。
これが基本です。これに則って行うわけですが、この問題の場合、対数をとることによって、1/nと∑が出せるわけです。そして、積分範囲に注意してくださいね。
<問題>
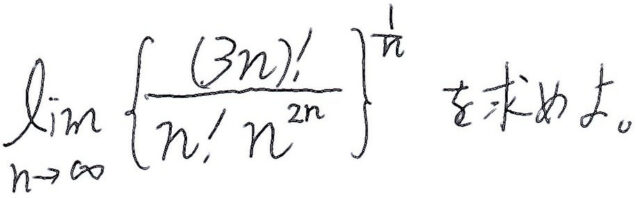 |

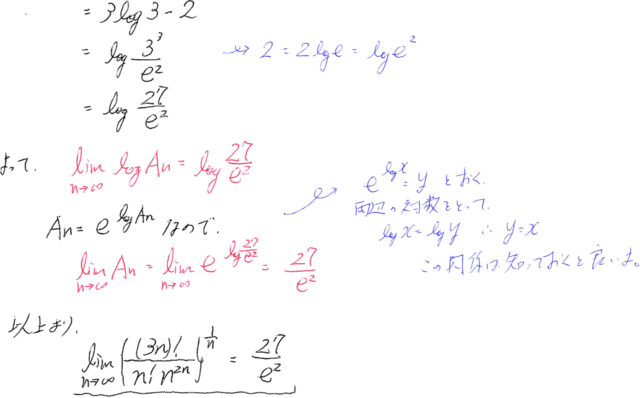
それでは、また、区分求積法の問題。
<問題>
|
中心が原点O、半径1の円を外接円とする正n角形がある。 各頂点をP0,P1,P2…Pn-1とし、この順に円周上に並んでいる。 x軸と線分OP0のなす角をΘとするとき。以下の極限を求めよ。 |
受験・学習に関する相談は、お気軽にお問合せフォームからどうぞ!受験生以外も、お待ちしてますよ♪
お問い合わせはこちら

