- カテゴリ
まずは、前回の数学（図形と方程式）の解説から！
前回の問題 数学（図形と方程式）
＜問題＞
|
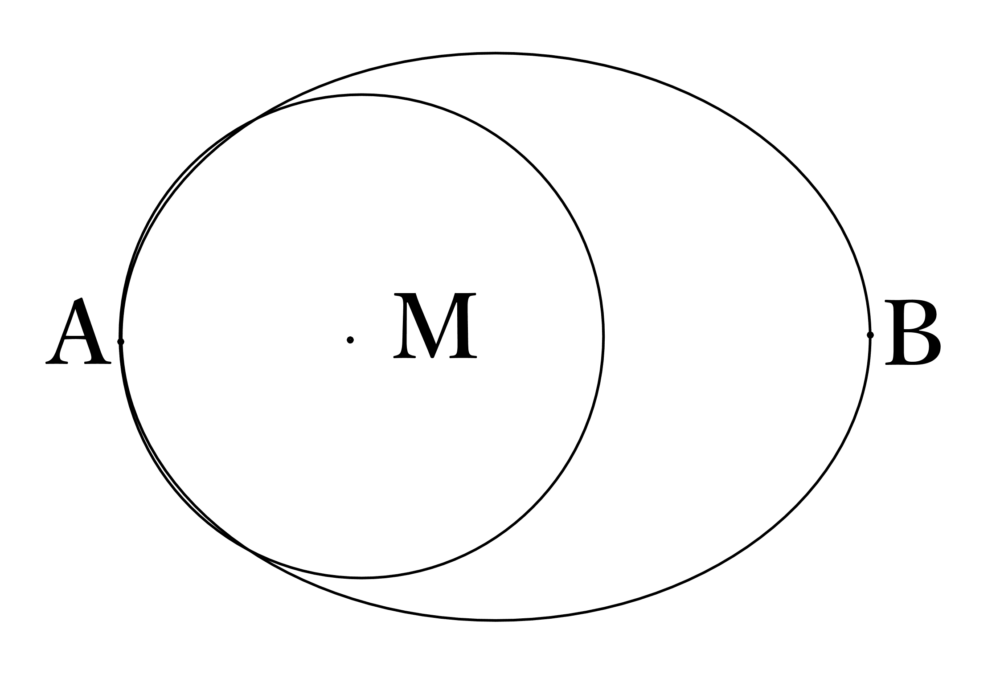
直線l：(1-k)x+(1+k)y+2k-4=0 はkの値によらず定点Aを通る。 （1）定点Aを求めよ。 （2）xy平面上に点Bをとる。原点Oと点Aと点Bを頂点とする三角形が正三角形になるとき、点Bの座標を求めよ。 （3）直線lと円 x2+y2=16の2つの交点を通る円Cが、2点(-4,0),(2,0)を通るとき、円Cの方程式を求めよ。 |
＜ヒント＞
（1）kについて整理しましょう。
（2）点Bは線分OAの中点Mを通り、直線OAに垂直な直線上にあること。又OMとBMの長さの関係を考えましょう。
（3）2つの図形の交点を通る図形の方程式の公式を利用しましょう。
＜解答＞
（2）は、図形と方程式の範囲で解きましたが、複素数平面を使って原点を中心に±60°の回転を考えてもOKですよ。
今週の問題 物理（万有引力）
＜問題＞
|
（1）宇宙ステーションの速さVを求めよ。 （2）図のAの位置で宇宙ステーションが人工衛星を進行方向に、ばねじかけで人工衛星を発射する場合を考える。ばねに蓄えられた弾性エネルギーをE、人工衛星の質量をm2、人工衛星発射後の宇宙ステーションの質量をm1（m1+m2=m）とする。発射直後の宇宙ステーション、人工衛星の速度をそれぞれV1、V2とするとき、運動量保存則とエネルギー保存則において成り立つ式をそれぞれ記せ。 （3）V1、V2をm1、m2、V、Eを用いて表せ。 （4）Ａ点で発射された人工衛星は図のような楕円運動し、天体か最も遠ざかる点Ｂで、天体からの距離が2r となる。点Ｂの位置での人工衛星の速さV’2をV2を用いて表せ。 （5）このような軌道をとるために必要な速さV2をG、M、rを用いて表せ。 （6）このとき、ばねの弾性エネルギーＥをG、M、r、m1、m2を用いて表せ。 |
＜ヒント＞
（1）運動方程式から求めましょう。
（3）（2）の連立方程式を解きましょう。
（4）ケプラーの第2法則（面積速度一定の法則）を利用しましょう。
（5）点Ａと点Ｂでの人工衛星のエネルギー保存則を考えましょう。
（6）（3）と（5）の結果を利用しましょう。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
