- カテゴリ
まずは、数学の解答・解説。
<問題>
|
xy平面で、原点Oを端とする半直線が、原点を中心に反時計回りに一定の角速度ωで回転している。その半直線上を動点Pが一定の速さvで動いている。但し、動点Pは、時刻t=0では原点Oにあり、半直線はx軸の正方向に一致する。 (1)線分OPとx軸のなす角をΘとすると、Θ=ωtであるが、そのときの点Pの位置をΘを用いて、媒介変数関数として表せ。 (2)0≦Θ≦πの範囲での、動点Pが描く曲線の概形を描け。 (3)0≦Θ≦πの範囲において、動点Pが描く曲線とx軸で囲まれた部分の面積を求めよ。 |
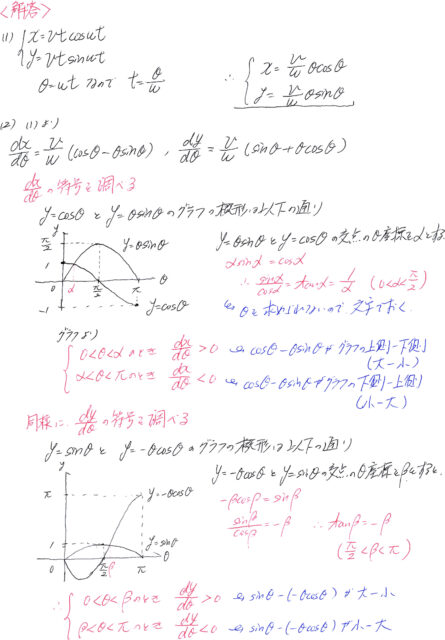



これは、大変な問題でした。お疲れ様。ポイントは面積を求めるときの処理だね。どっち方向に積み上げたら簡単なの?を考えると良いです。
では、今回も数学。今度は体積ね。
<問題>
|
xy平面において、曲線y=exと3直線y=-x+1とy=-x+e+1とy=xで囲まれた部分をy=xを軸として回転させてできる立体の体積を求めよ。 |
<ヒント>
x軸やy軸のまわりを回転する問題なら、当然、見慣れていると思う。でも、今回はそうじゃない。考え方としては、回転体をy=xに垂直になるように輪切りにして、その断面の面積をy=xの方向に積み上げれば良いのです。そのための手順を簡単に説明。
- y=ex上の点をP(t,et)とおいて、点Pからy=xに下した垂線の足を点Qとして、線分PQの長さを求める。これが、断面の円の半径だね。(当然、tの関数になるよ。)
- 原点Oと点Qを結ぶ線分OQの長さXをtを用いて表す。
- Xというのが積み上げ方向になるので、π∫PQ2dXを計算。(積分範囲は自分で考えてね。でも、結局、置換積分をするので、文字で置いておけばOK。)
- あとは、計算するのみ。勿論だけど、部分積分はやらなきゃならない。
受験・学習に関する相談は、お気軽にお問合せフォームからどうぞ!生徒さん本人でも、親御さんでも、お受けします。お待ちしています!!
お問い合わせはこちら

