高校範囲の数学・物理・化学の公式を解説して行こう思います。堅く苦しい感じではなく、くだけた感じで説明して行きますね。なので、ぽんすけ（ライオンのぬいぐるみ、新着情報一覧で見ると写真があるよ。）というウチのマスコットに登場してもらいます。題して、ぽんすけの「数物化の公式解説」

　1回目の公式は、自然対数の底e（ネイピア数）について。「e＝2.718…この値は覚えて！y=e^xは微分しても変わらないから！」と受験生のとき、学校の授業でにいきなり言われたっけな～。訳も分からず、暗記だけはしましたよ。それでも、普通より少し上くらいのレベルの問題なら、太刀打ちできた！でもね～。応用問題とか、定義の芯を喰った問題は、全滅でしたね。まさに、手が出ない！お手上げ！内角シュートで身体を起こされた後の外角低めのスピンの効いたストレートって感じっす。

　まず、なんでe=2.718…なのか？およそ2.72は、知っていた方が良いのは、確かに事実なんだけど…。ここを、まず説明。

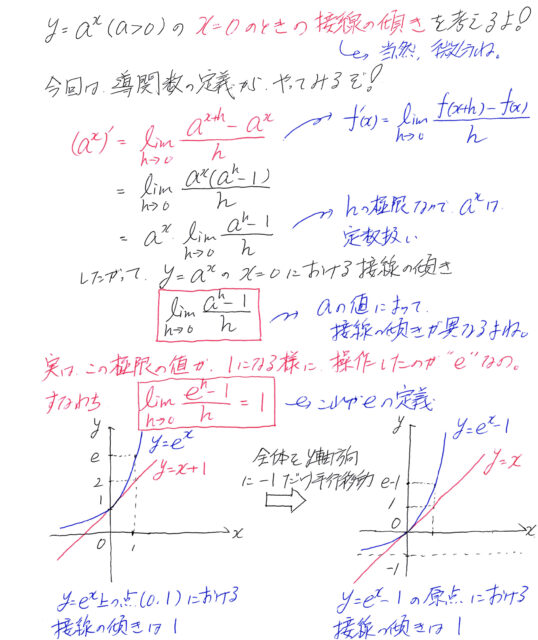
　つまり、x＝0における接線の傾きが1になるような指数関数の底がeなの。都合の良いように仕組まれた数なんですよ！y=e^xを微分しても、変わらないのも、これが理由。（手書きの上から3行目の式でa=eのとき、極限の値が1になるから。）まあ、便利で重要な数なんですけどね。1になるっていうこと自体、ものすごーく利便性があるのよ。

　上の赤字かつ赤囲みの式は、高得点を取りたいなら、覚えるというよりか、原点付近のグラフのイメージ像を頭の中で描けるように、変形に時間が掛からないようにしておくべき！これを理解すると、実践での使いどころが分かってくるんですよ。式の形で言うと、（1+0)^∞の形のときは、eが怪しい～！（くだらんダジャレだ）そう思ってね。

　数学・物理・化学の公式で疑問に思うこと、その他色々、答えられないこともあるけど、可能な限り答えます！（ビシッ！！）問い合わせフォームからお気軽にどうぞ。