- カテゴリ
まずは、前回の数学(数列)の解説からです。
先週の問題 数学(数列)
<問題>
|
次の漸化式を満たす数列anの一般式を求めよ。 (1)a1=0,a2=1,an+2-5an+1+6an=0 (2)a1=0,a2=1,an+2-6an+1+9an=0 |
<ヒント>
(1)特定方程式t2-5t+6=0を解いて処理しましょう。
(2)基本的には(1)と同じですが、特性方程式が重解になるので・・・
<解答>

3項間の漸化式の基本パターンです。特性方程式が重解の場合も解けるようにしておきましょう。
今週の問題 物理(数列)
<問題>
|
(1)TB=3T0のとき、温度TAを求めよ。 (2)(1)のとき、A室、B室合計の理想気体の内部エネルギーの変化量を気体定数R[J/mol·K]を用いて表せ。 |
<ヒント>
(1)B室での変化は断熱変化になるので、ポアソンの式(PVγ=一定、又はTVγ-1=一定)を利用。これと、ボイル・シャルルの法則で解き進めましょう。
(2)(1)の結果から求めましょう。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら

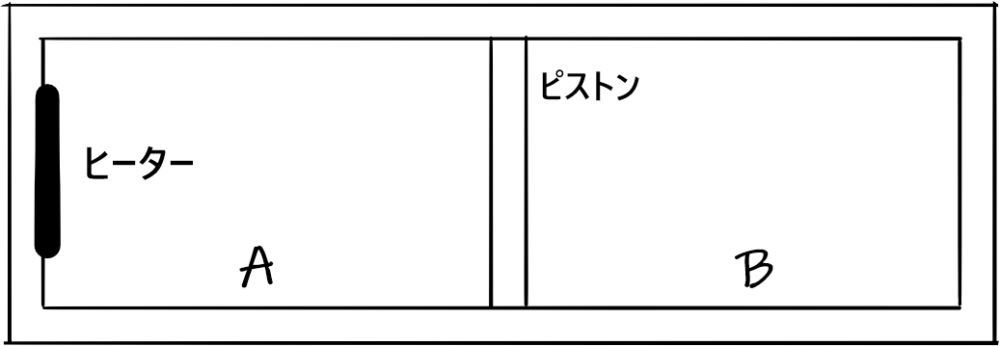 図に示すようなシリンダー内をなめらかに動くピストンで、A室とB室に分ける。n[mol]の単原子分子理想気体が、A室、B室に封入されている。最初は、共に、圧力P0[N/m2]、体積V0[m3]、温度T0[K]であり、シリンダー容器、ピストンは熱を伝えないものとする。ヒータで加熱したら、A室、B室の温度は、それぞれTA[K]、TB[K]となった。このとき、ピストンは右に動き、A室の理想気体は、熱を得るとともにB室に対して仕事をするものとする。
図に示すようなシリンダー内をなめらかに動くピストンで、A室とB室に分ける。n[mol]の単原子分子理想気体が、A室、B室に封入されている。最初は、共に、圧力P0[N/m2]、体積V0[m3]、温度T0[K]であり、シリンダー容器、ピストンは熱を伝えないものとする。ヒータで加熱したら、A室、B室の温度は、それぞれTA[K]、TB[K]となった。このとき、ピストンは右に動き、A室の理想気体は、熱を得るとともにB室に対して仕事をするものとする。