- カテゴリ
まずは、前回の数学(軌跡)の解説から!
前回の問題 数学(軌跡)
<問題>
|
実数a,bがa2+b2+2a+2b=0を満たして変化している。このとき、点(a+b,ab)が描く軌跡を図示せよ。 |
<ヒント>
x=a+b,y=abと置いて、a,bを消去すれば良いのですが、それだけでは不完全です。tの2次方程式(t以外の文字でも構わないです)t2-xt+y=0の解はt=a,bとなるので、実数解を持たなければなりませんよね。このことを利用しましょう。
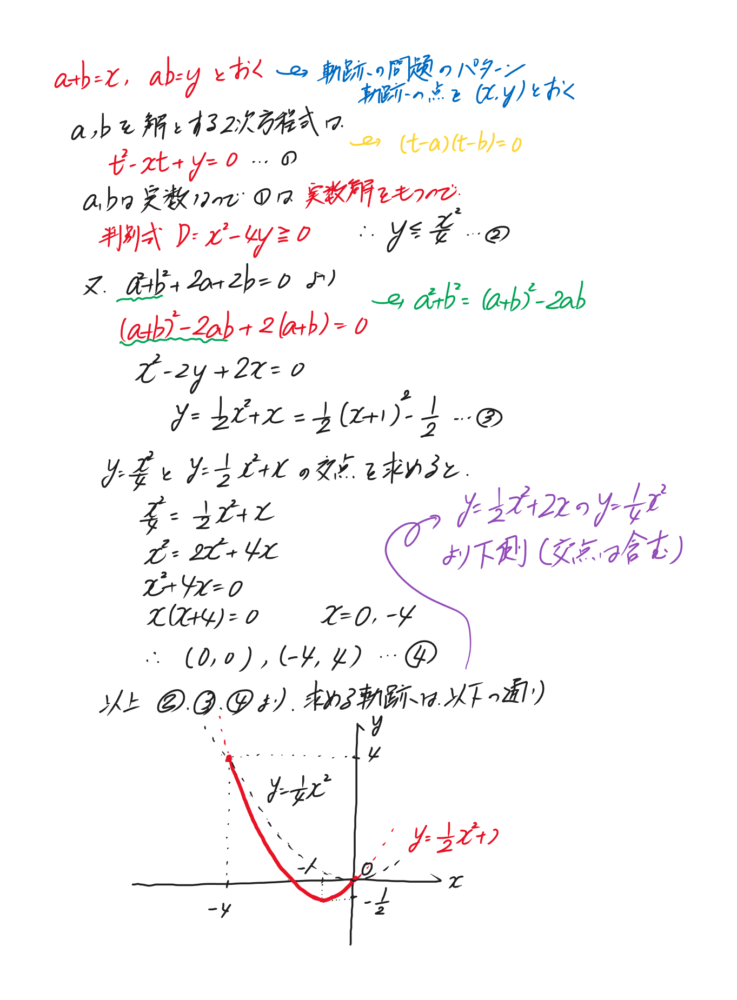
<解答>
恐らく、上の解答の③の式はほとんどの人が導き出せると思います。難しいのは②を導き出すことです。これは、a,bが実数であるということ、軌跡上の点の座標がa,bの和と積で表されていることから解と係数の関係を利用して二次方程式が実数解を持つことを利用するわけです。「実数」という言葉が出てきたら、そこに注意を払うようにして下さいね。
今週の問題 数学(対数)
<問題>
|
xの方程式 (log10x)2-log10x3+(t2+1)=0が異なる2つの実数解α,βをもつ。 (1)実数tの取り得る値の範囲を求めよ。 (2)logαβ+logβαの取り得る値の範囲を求めよ。 |
<ヒント>
log10α=A,log10β=BとおくとA,BはXの2次方程式 X2-3X+(t2+1)=0の異なる2つの実数解となるので、そこから(1)は解きましょう。(2)は底の変換をして(1)を利用です。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら