- カテゴリ
まずは、前回の数学（微分法（数学Ⅱ））の解説から！
前回の問題 数学（微分法（数学Ⅱ））
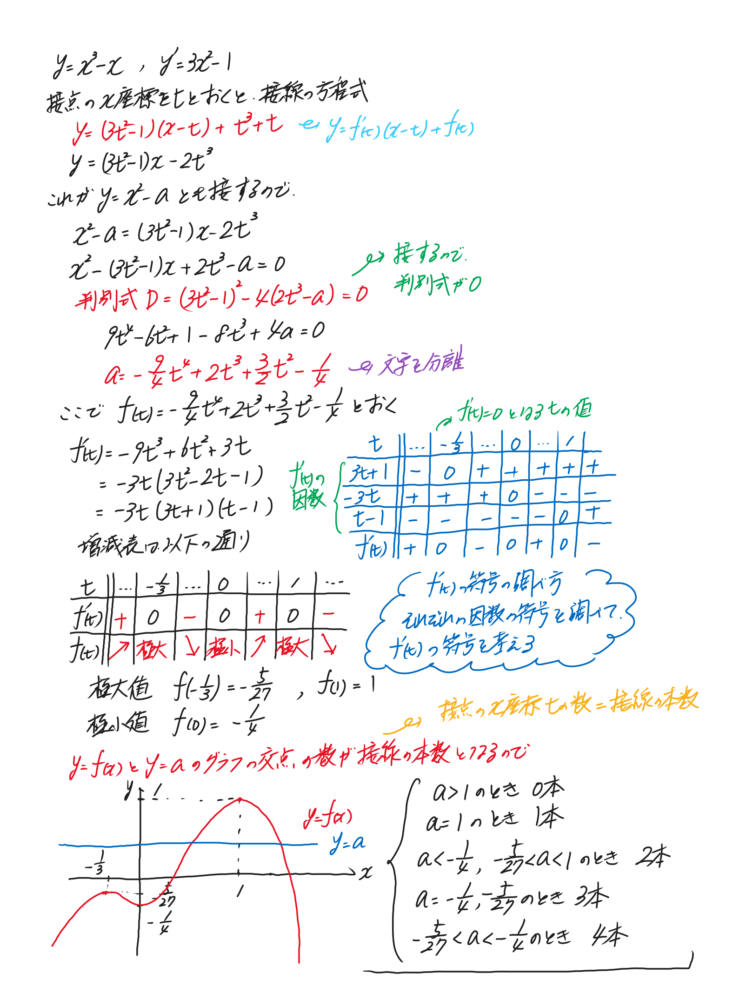
＜問題＞
|
2曲線y=x3-xとy=x2-aの両方に接する直線の本数をもとめよ。但し、aは定数とする。 |
＜ヒント＞
まずは、y=x3-xの接点のx座標をtとおいて、接線の方程式を求めましょう。それがy=x2-aと接することを利用して2次方程式の判別式を考えましょう。
＜解答＞
方程式の解の個数はグラフの交点の数の関係の典型的な問題です。文字を分離して、f(x)=定数の形にして、交点の数を調べましょう。
今週の問題 物理（波動）
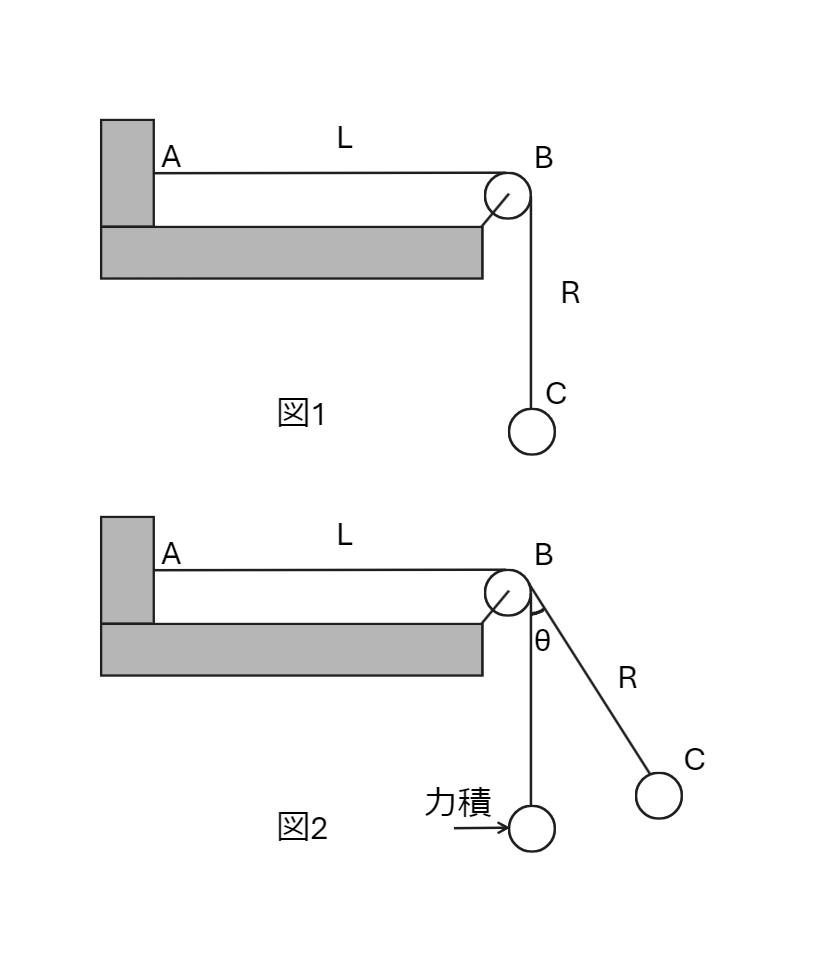
＜問題＞
|
（1）AB間を弾いたところ、基本振動が起こった。このときの振動数f0をm,g,L,σを用いて表せ。 次におもりCに対して、図2の様に水平方向に力積を加えて鉛直面内で振動させた。このときBC間の鉛直線となす角θの最大角はθ0であった。ただし、θ0は鋭角である。 （2）金属線の張力Sを触れ角のθの関数として、m,g,θ,θ0を用いて表せ。 （3）弦ABの基本振動fをθの関数として、f0,θ,θ0求めよ。 （4）おもりCが振れている間、振動数は1オクターブに渡って変化した。θ0を求めよ。但し1オクターブは振動数比が2である。 |
＜ヒント＞
（1）基本振動の波長は2L、弦を伝わる波の速度Vは張力をSとするとV=(S/σ)1/2であり、V=fλの関係を利用して求める。
（2）おもりのエネルギー保存則と向心成分の運動方程式からSを求める。
（3）（1）と（2）の結果を利用する。
（4）（3）の最小値と最大値を求め、その比が2であることを利用する。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
