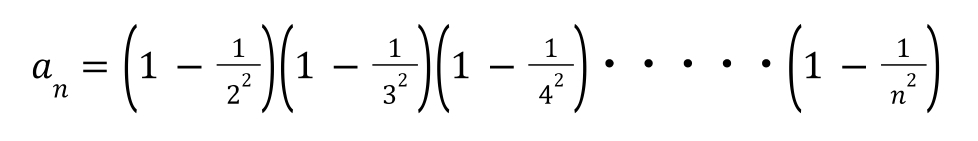---

　まずは、前回の数学（極限）の解説から！

前回の問題　数学（極限）

＜問題＞

次の数列{an}の極限を求めよ。

＜ヒント＞

掛け算の極限を考えるのは、難しいものがあるので、これを足し算や引き算に換える方法を考えましょう。すなわち、両辺の対数をとって考えましょう。底は何でも構いません。

＜解答＞

 対数をとって処理することがミソになります。対数はかけ算を足し算にする方法なので、積の形の極限では両辺の対数をとるということは、良くなされることです。

今週の問題　物理（コンデンサー）

＜問題＞

真空中に平行な2枚の極板があり、その距離はd[m]、面積はS[m2]のコンデンサーがある。はじめに電源につないで、極板間の電位差をVとして、充電を完了した。以下の問いに、d、S、V、⊿d、真空の誘電率ε0だけを用いて答えよ。 （1）極板間に生じる電界の強さEを求めよ。 （2）極板に蓄えられる電気量Q を求めよ。 （3）コンデンサーの蓄えられる静電エネルギーUを求めよ。 次に電源をはずして、極板間の距離を⊿dだけ広げた。 （4）コンデンサーに蓄えられるエネルギーの増加分⊿Uを求めよ。 （5）コンデンサーの極板間にはたらく引力Fの大きさを求めよ。

＜ヒント＞

　コンデンサーの公式ではなく、仕組み、原理を考えましょう。充電完了後、向かい合う極板は符号で同じ大きさの電荷を帯び、その結果、極板内部の電場は0となり、電荷の移動がない、すなわち、それが充電完了を意味することを理解してくださいね。極板間の電場が分かれば、（1）～（3）は解けます。（4）は電源を外すので、極板間の電位差は変化しますが、電気量保存則から蓄えている電荷の変化はありません。そのことを考えて下さいね。

　学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。