まずは、先週の数学の解説から！

先週の問題　数学㉗（変曲点）

＜問題＞

y=xe-xについて、 （1）変曲点における接線の方程式を求めよ。 （2）y=xe-xと（1）の接線とy軸で囲まれた部分の面積を求めよ。 （3）y=xe-xと（1）の接線とy軸で囲まれた部分をx軸を中心に回転させてできる立体の体積を求めよ。

＜ヒント＞

（1）当然、1回微分、2回微分をして、増減表を書くわけです。

（2）グラフの上側－下側の積分をします。積分範囲は、グラフの概形を描けばわかりますからね。

（3）回転体の体積の求め方で、計算するのみです。

＜解答＞

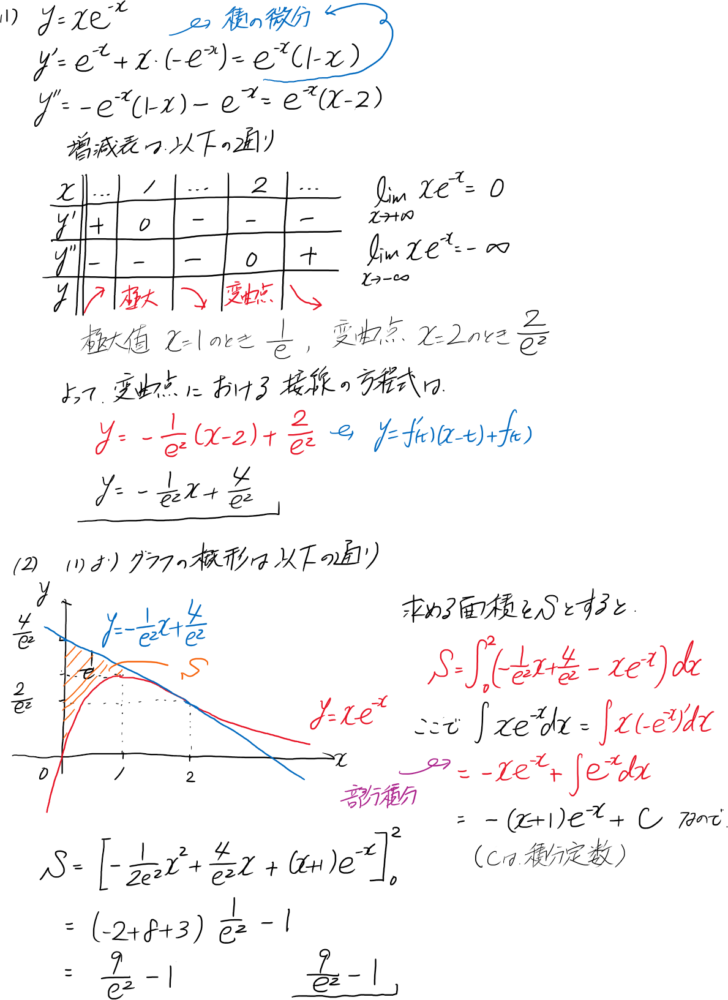
なかなか、骨が折れる計算でしたね。でも、頑張ってカリカリと手を動かしましょう。

今週の問題　数学㉘（面積と回転体の体積）

＜問題＞

（1）不定積分　I=∫e-xsinxdxを求めよ。 （2）0≤x≤2πの範囲で、y=e-xsinxとx軸で囲まれた部分の面積を求めよ。 （3）0≤x≤2πの範囲で、y=e-xsinxとx軸で囲まれた部分をx軸を中心に回転してできる立体の体積を求めよ。

＜ヒント＞

（1）部分積分を利用しよう。

（2）（1）の結果を利用。

（3）回転体の体積を求めるわけだけど、頑張って計算だ！

今回も、計算が大変ですが、頑張りましょう。

学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。