- カテゴリ
まずは、先週の数学の解説から!
先週の問題 数学㉘(面積と回転体の体積)
<問題>
|
(1)不定積分 I=∫e-xsinxdxを求めよ。 (2)0≤x≤2πの範囲で、y=e-xsinxとx軸で囲まれた部分の面積を求めよ。 (3)0≤x≤2πの範囲で、y=e-xsinxとx軸で囲まれた部分をx軸を中心に回転してできる立体の体積を求めよ。 |
<ヒント>
(1)部分積分を利用しよう。
(2)(1)の結果を利用。
(3)回転体の体積を求めるわけだけど、頑張って計算だ!
<解答>
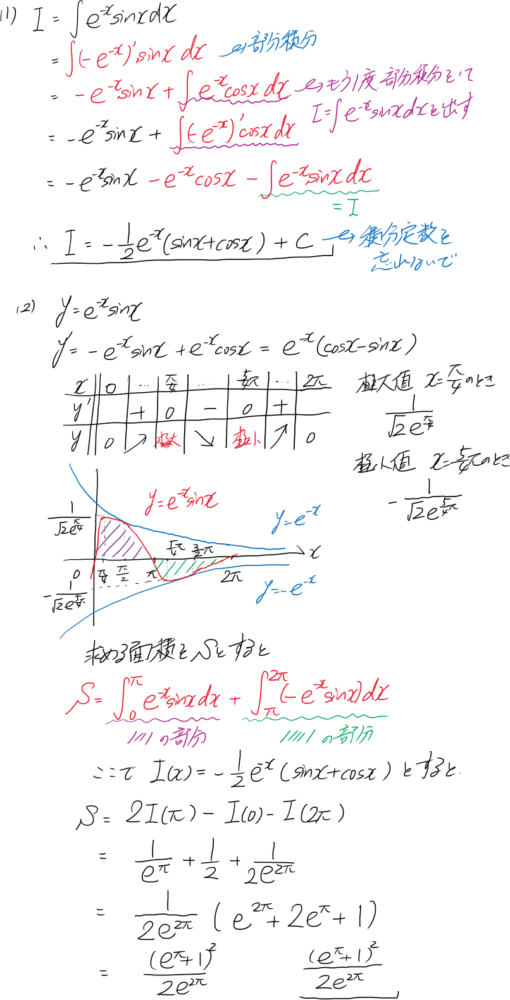

部分積分は、練習して慣れて下さいね。それでは今週の問題。今回は、物理(気体)です。
今週の問題 物理⑭(気体)
<問題>
|
(1)理想気体が圧力P0、体積V0、温度T0のときの、ピストンにかかるばねの力を求めよ。 (2)温度Tでのシリンダー内の圧力を求めよ。 (3)理想気体の温度がT0のときのばねの伸びを求めよ。 |
<ヒント>
(1)ばねの弾性力をfとおいて、ピストンの運動方程式(つり合いの式)を立てる。
(2)ばねは自然長なのでf=0
(3)ボイル・シャルルの法則を使おう。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら

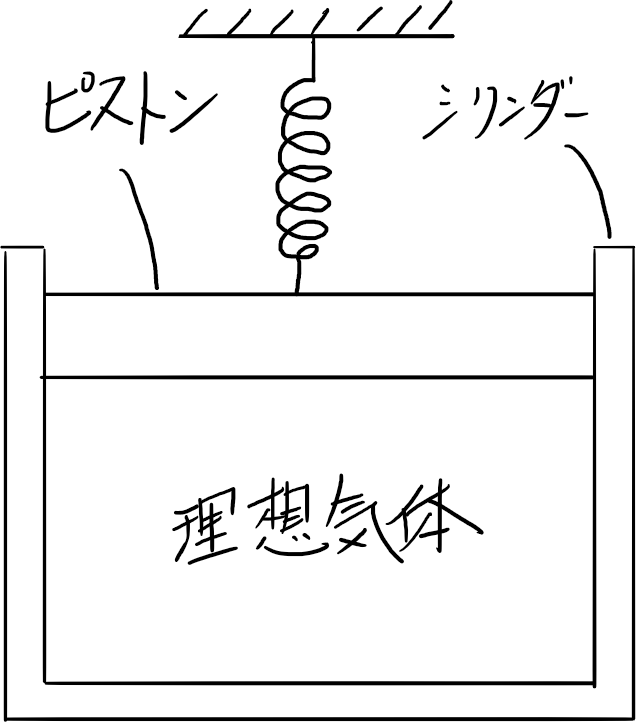 図のように、真空中で鉛直に置かれたシリンダーの中に、断面積S、質量Mのなめらかに動くピストンがあり、ばねで吊り下げられている。シリンダー内は、理想気体が入っており、圧力P0、体積V0、温度T0でつり合っている。シリンダー内の温度をTに上昇すると、ばねは自然長になった。重量加速度をg、ばねの質量は無視できるものとし、以下の問いに答よ。
図のように、真空中で鉛直に置かれたシリンダーの中に、断面積S、質量Mのなめらかに動くピストンがあり、ばねで吊り下げられている。シリンダー内は、理想気体が入っており、圧力P0、体積V0、温度T0でつり合っている。シリンダー内の温度をTに上昇すると、ばねは自然長になった。重量加速度をg、ばねの質量は無視できるものとし、以下の問いに答よ。