- カテゴリ
まずは、先週の数学(三角関数)の解説からです。
先週の問題 数学㊱(三角関数)
<問題>
実数x,yが、5x2+3xy+y2=1を満たすとき、x2+y2の取り得る値の範囲を求めよ。
<ヒント>
x=rcosθ,y=rsinθと極座標変換してみよう。そのあとの三角関数の合成をするのですが、その前に・・・。それは、自分で考えましょう。
<解答>

まず、極座標変換することが、難しいと思います。x2+y2が円を表すことが分かれば、できると思いますが、そうでなければ難しい問題です。大学だと偏微分というものを習うのですが、それを使うと比較的簡単に解けます。それでは、今週は物理、運動方程式です。
今週の問題 物理(運動方程式)
<問題>
|
(1)台Aの加速度をa(右向きを正)、Bの加速度をb(右向きを正)、cの水平成分の加速度をc1(右向きを正)、鉛直成分の加速度をc2(下向きを正)として、A、Bの水平成分とcの水平成分と鉛直成分の運動方程式を記せ。但し、糸の張力をT、穴の両側の壁がCに及ぼす垂直抗力をN(右向きを正)とする。 (2)糸が伸び縮しないこと、Cが穴の中を滑ることから、c1,c2をa,bで表せ。 (3)F=0のとき、Bの加速度を求めよ。 (4)F=0のとき、Cが下の床面に達するまでに台Aが移動した距離を求めよ。 |
<ヒント>
(1)働く力を図示して、物体ごと、成分ごとに運動方程式を立てます。作用反作用に注意しましょう。因みにAにも滑車を貸して糸の張力と同じ大きさの力は働いていますよ。
(2)これは自力で考えて欲しい。
(3)(1)と(2)からa,c1,c2とT,Nを消去して求めよう。
(4)c2とaの比から考えると楽ですよ。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。

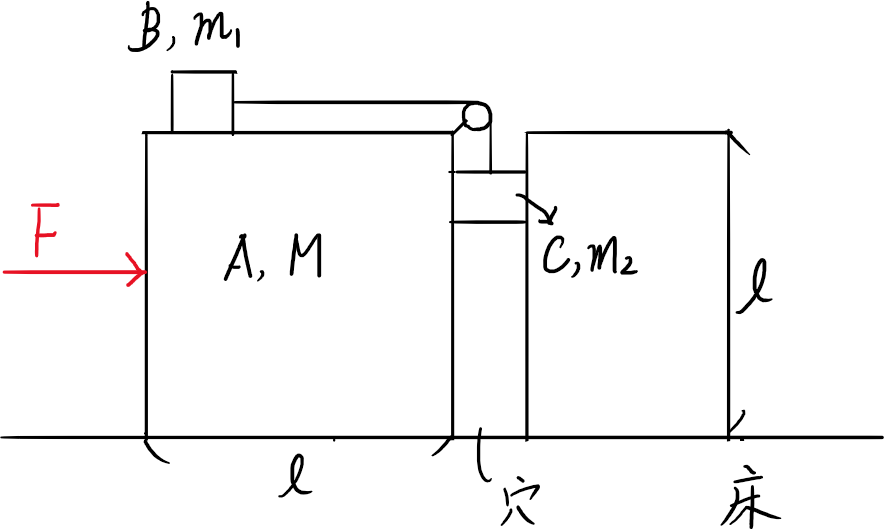 図のように、台A(質量M)の上をB(質量m1)がなめらかに滑り、C(質量m2)は台の中の鉛直にくり抜いた穴をなめらかに滑る。(水平成分におけるAとCの速度は常に同じ)台Aの高さと台の左端から穴までの距離は共にl、(Cの変位の鉛直成分の範囲は、下向きを正として0≤yB≤l)BとCは台Aに固定された滑車を介して伸び縮みしない糸でつながっている。又、Bが台の左端にあるとき、Cは穴の一番上にあり、糸はピンと張っていた。台の左端にBを置き、台Aを滑らかな水平面をもつ床に置き、に力Fを右向きに加える。重力加速度の大きさをg、滑車と糸の質量は無視して、以下の問いに答よ。
図のように、台A(質量M)の上をB(質量m1)がなめらかに滑り、C(質量m2)は台の中の鉛直にくり抜いた穴をなめらかに滑る。(水平成分におけるAとCの速度は常に同じ)台Aの高さと台の左端から穴までの距離は共にl、(Cの変位の鉛直成分の範囲は、下向きを正として0≤yB≤l)BとCは台Aに固定された滑車を介して伸び縮みしない糸でつながっている。又、Bが台の左端にあるとき、Cは穴の一番上にあり、糸はピンと張っていた。台の左端にBを置き、台Aを滑らかな水平面をもつ床に置き、に力Fを右向きに加える。重力加速度の大きさをg、滑車と糸の質量は無視して、以下の問いに答よ。