- カテゴリ
まずは、数学、関数方程式の解答。
<問題>
|
f(x)は、x>0で定義された関数であり、x=1で微分可能である。また、f’(1)=2であり、任意の正の数で以下の式が常に成り立つ。 f(xy)=f(x)+f(y) (1)f(1)の値を求めよ。 (2)f(1/x)をf(x)で表せ。 (3)f(x/y)をf(x)とf(y)で表せ。 (4)f(x)は、任意のx(>0)に対して、微分可能であることを示せ。 (5)f(x)を求めよ。 |
<ヒント>
(1)これは、x=y=1を代入してみて。パズル感覚で解いていく感じでね。
(2)(1)の結果を利用。
(3)与式と(2)の結果を利用。
(4)ある点で微分可能というのは、滑らかに連続ということなので、その点での接線が引けるということ。つまり、導関数が存在することね。つまりだ、f'(x)が存在することを示せばよいわけ。
(5)(4)の結果から。


今回の問題は、導関数の定義を利用しないと無理です。やはり、定義とか定理と言うものは、しっかりと押さえなければなりません。曖昧だとダメなんです。根本的なものほど、明確にさせなければいけません。逆に、応用的なものはふあ~っとしてても大丈夫。いや、応用と言うのは、その場で良い様に形を変えて利用するものなので、型に嵌めるべきではありません。自由な発想は、天才君ではない限り、基礎的なこと、基本的なことが、理屈がわかっていないと、生まれてこないものですよ。
そして、今回は、物理です。交流です。RLC回路です。今回の問題は、面倒くさい問題です。手間が掛かります。でも、カリカリと計算して下さいね。回路の問題は、前にも述べましたが、回路の方程式と、キルヒホッフの法則(第一・第二)(第二法則が回路の方程式だけどね。)それと、定常状態とか電荷Qと電流Iの関係や初期条件をきちんと処理すれば、大体は何とかなります。因みに、交流については、公式解説でまだしてないので、そのうちしますね。では、問題。
<問題>
|
(1)K3は開いたまま、K1,K2を閉じて定常状態になったときのコイルに流れる電流を求めよ。 (2)K2は開いたまま、K1,K3を閉じて定常状態になったときのコンデンサーに蓄えられた電荷とエネルギーを求めよ。 (3)K1,K2,K3を閉じて定常状態になった後、K1を開く。 a)K1を開いた直後、コイルとコンデンサーを含む閉回路では、エネルギーはどこに蓄えられているか? b)この閉回路では周期的に交流電流が流れることになる。その周期を求めよ。 (4)(3)の状態において、コンデンサーの最大電圧を求めよ。 (5)(3)の状態において、コイルを流れる電流と図に示したN点のM点に対する電位をグラフに描け。但し、横軸は時間とし、M→コイル→Nの向きを正とする。 |
<ヒント>
(1)定常状態では、dIL/dt=0
(2)定常状態、すなわち、コンデンサーが充電完了状態になると、コンデンサーに電流は流れない。だから、IC=0
(3)(4)(5)回路の方程式とI=dQ/dtの関係、そして初期条件を手間が掛かっても処理する。(4)ができれば、自ずと(5)は出来ますよ。
質問等があれば、遠慮なく問い合わせフォームからどうぞ!!

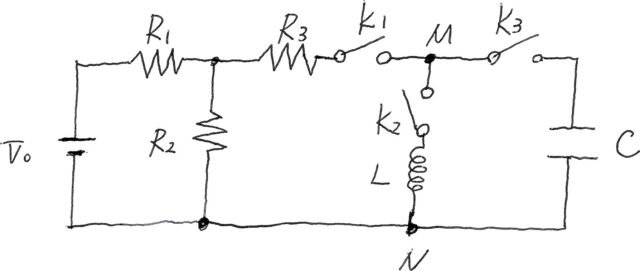 図の電気回路は、起電力VOの直流電源、抵抗値R1,R2,R3の電気抵抗、自己インダクタンスLのコイル、電気容量Cのコンデンサー、及び、スイッチK1,K2,K3から構成されている。電源とコイルの内部抵抗は無視し、導線の抵抗はないものとする。以下の問いに答えよ。
図の電気回路は、起電力VOの直流電源、抵抗値R1,R2,R3の電気抵抗、自己インダクタンスLのコイル、電気容量Cのコンデンサー、及び、スイッチK1,K2,K3から構成されている。電源とコイルの内部抵抗は無視し、導線の抵抗はないものとする。以下の問いに答えよ。