- カテゴリ
先週の解答から、行きます!計算が面倒だったと思うけど、そこは頑張るしかないです。選択肢は、「頑張る」と「もっと頑張る」の2つです。「頑張らない」はありません。By 筋肉体操。あれ、YouTubeでたまに、見てやってますけど、笑ってしまうね。金八先生じゃない武田先生の方が、僕的には、尊敬しています。
先週の解答(数学 空間ベクトル)
<問題>
 |
<ヒント>
3点を通る平面上にある点の位置ベクトルは、その3点の位置ベクトルの係数の和=1の関係があったね。
(1)は、それを利用だ。
(2)も、O,H,Pの3点が同一直線上にあることと、(1)で言ったことを利用。
(3)(2)を利用です。
(4)これは(3)のおまけになります。
解答


空間ベクトルは、平面ベクトルに比べると、3つのベクトルで空間の点の位置ベクトルを表すし、成分が増える分、方程式を解く手間が掛かりますよね。でも、考え方は平面ベクトルのときとほぼ同様です。では、今回は物理の交流回路。もう少し、交流に慣れましょうね。
今週の問題(物理 交流回路(RLC回路))
<問題>
|
(1)このとき、固定抵抗に流れる電流の実効値を、V0、R、L、ωを用いて答えよ。 (2)このとき、コンデンサー流れる電流の実効値を、V0、r、C、ωを用いて答えよ。 (3)このとき、rの値をR、C、Lを用いて答えよ。 (4)このとき、回路全体のインピーダンスをR、C、L、ωを用いて答えよ。 |
<ヒント>
(1)電源→R→L→電源の閉回路において、回路の方程式を立てて、I=I0sin(ωt+Θ)とでも置けばよい。
(2)(1)と同様に、電源→C→r→電源の閉回路におて、回路の方程式を立てる。計算上i=i0cos(ωt+Φ)と置いた方が楽かな。因みに、波の式(振動の式)は、正弦でも余弦でもどちらで置いてもOKですよ。
(3)(1)と(2)の結果と閉回路R→G→C→Rの回路の方程式を考えてみて。
(4)(3)までのことから、全電流を求めれば、インピーダンス(抵抗に相当する)は導けるね。
それでは、頑張って下さいね。
受験や学習の相談をお待ちしています。気軽に問い合わせフォームからどうぞ!

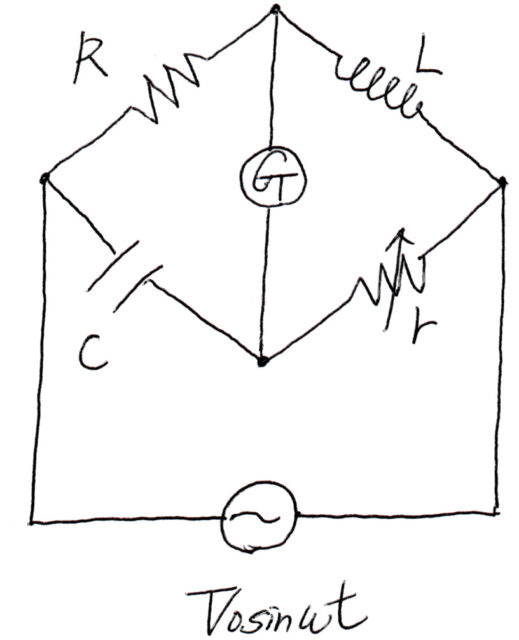 図の交流ブリッジ回路において、固定抵抗の抵抗値をR、コイルの自己インダクタンスをL、コンデンサーの電気容量をC、外部電源の起電力をV0sinωtとする。可変抵抗rの値を変えて行くと、rがある値で検流計Gに電流が流れなくなる。
図の交流ブリッジ回路において、固定抵抗の抵抗値をR、コイルの自己インダクタンスをL、コンデンサーの電気容量をC、外部電源の起電力をV0sinωtとする。可変抵抗rの値を変えて行くと、rがある値で検流計Gに電流が流れなくなる。