- カテゴリ
まずは、先週の数学の解説から!
先週の問題 数学㉜(数列の和)
<問題>
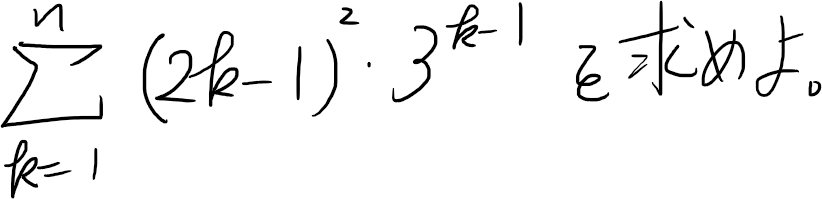 |
<ヒント>
等差数列×等比数列の和の応用です。まずは、書き下して、公比の3をかけたものを引きましょう。そうすれば、何とかなるはずです。
<解答>

計算は面倒だけど、頑張ってやってくださいね。それでは、今週は物理です。
今週の問題 物理⑯()
<問題>
|
(1)状態BとCの温度をそれぞれ答よ。 (2)A→Bの変化において、気体が外部から受けた仕事と気体が吸収した熱量を求めよ。 (3)B→Cの変化において、気体が外部から受けた仕事と気体が吸収した熱量を求めよ。 (4)C→Aの変化において、気体が外部から受けた仕事と気体が吸収した熱量を求めよ。 (5)A→B→C→Aのサイクルの熱効率(気体が外部へした仕事と吸収した熱量の比)を求めよ。 (6)変化B→Cにおいて、その間の最高温度を求めよ。 |
<ヒント>
(1)ボイル・シャルルの法則を利用します。
(2)(3)(4)熱力学の第一法則と理想気体の状態方程式を使います。
(5)(2)~(4)の結果を利用
(6)直線BCの式を求めて、理想気体の状態方程式を用いて、Pを消去してTを求めましょう。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。
お問い合わせはこちら

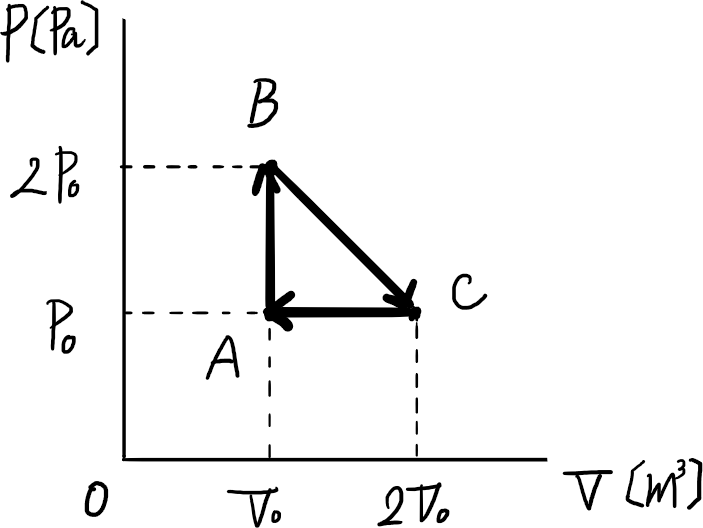 1molの単原子分子の理想気体を図の様にA→B→C→Aに沿って、直線経路でゆっくり変化させた。状態Aの温度はT₀[K]である。気体定数R[J/mol・K]とT₀[K]を用いて以下の問いに答よ。
1molの単原子分子の理想気体を図の様にA→B→C→Aに沿って、直線経路でゆっくり変化させた。状態Aの温度はT₀[K]である。気体定数R[J/mol・K]とT₀[K]を用いて以下の問いに答よ。