- カテゴリ
まずは、前回の数学(領域)の解説からです。
先週の問題 数学㊷(三角関数)
<問題>
|
0<θ<πとする。4sinθcosθcos3θ=sin3θを満たすとき、sinθ、sin2θ、sin4θの値を求めよ。 |
<ヒント>
3倍角の公式を利用して、cos3θ、sin3θを直しましょう。そして、頑張ってsinθだけの式にして、sinθの高次方程式を解きましょう。その後は、2倍角の公式を利用して、sin2θとsin2θの値を求めます。
<解答>

正直、計算が少しばかり面倒でしたね。でも、このくらいは苦にならずできるようにして下さい。計算力を鍛えれば、それだけ試験では有利です。
今週の問題 物理㉑(力学の保存則)
<問題>
|
(1)小球の速度の水平成分をv、台の速度Vとするとき、Vをvで表せ。 (2)小球が最初に台の壁に衝突する直前の小球の速度v1と台の速度V1を求めよ。 (3)小球が最初に台の壁に衝突する直後の小球の速度v’1と台の速度V’1を求めよ。 (4)1回目の衝突で失われた力学的エネルギーを求めよ。 (5)小球が最初に台の壁に衝突した後、小球が到達する最高点の高さを求めよ。 |
<ヒント>
(1)運動量保存則から求めます。
(2)(1)と力学的エネルギー保存則から求めます。
(3)はね返り係数と(1)の結果から。
(4)(2)と(3)を利用。
(5)(4)と力学的エネルギー保存則を利用。
とにかく、カリカリと計算して頑張りましょう。
学習や進路に対する質問等は、お気軽に問い合わせフォームからどうぞ。お待ちしています。

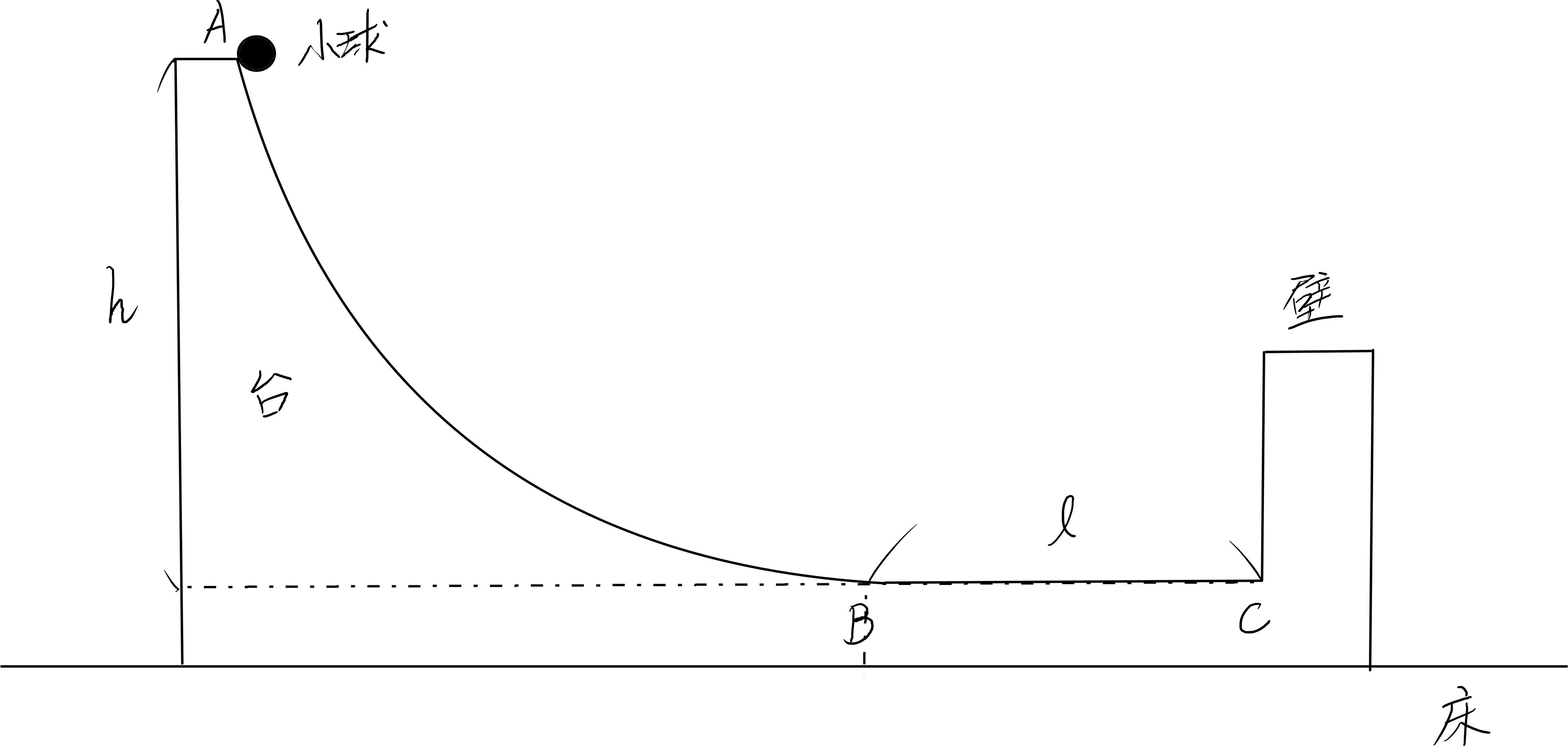 図のように、なめらかな斜面ABと水平面BCがなめらかにつながり、垂直な壁を持つ質量Mの台が水平な床の上で静止している。BC間の距離はlで、水平面BCからの高さがhである点Aから質量mの小球を斜面ABに初速度0で滑らせる。小球と台の壁とは垂直に衝突し、はね返り係数はeである。小球の運動は、図に表した紙面内でのみするものとし、重力加速度をg、台は固定されておらず、床と台の間に摩擦ははたらかないものとし、台は床から離れないものとする。又、速度は床に対するものとする。
図のように、なめらかな斜面ABと水平面BCがなめらかにつながり、垂直な壁を持つ質量Mの台が水平な床の上で静止している。BC間の距離はlで、水平面BCからの高さがhである点Aから質量mの小球を斜面ABに初速度0で滑らせる。小球と台の壁とは垂直に衝突し、はね返り係数はeである。小球の運動は、図に表した紙面内でのみするものとし、重力加速度をg、台は固定されておらず、床と台の間に摩擦ははたらかないものとし、台は床から離れないものとする。又、速度は床に対するものとする。